干货满满｜A-level数学微积分之函数增减性

　　今天为大家整理了一波关于函数增减性的知识点，正在学习A-level数学的小伙伴们赶紧收藏起来～

　　1. Increasing and Decreasing Functions  增函数与减函数

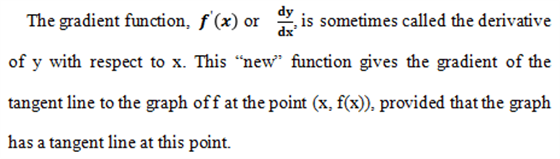
　　导数是函数的斜率组成的新函数，可以得到过曲线上任一点的切线斜率。可以说导数决定了函数的增减性，函数的增减性也决定这导数的正负。

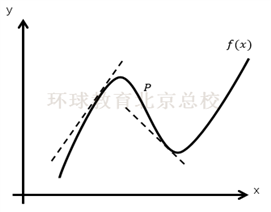
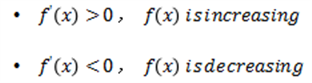
　　当导数大于零，函数是增函数；当导数小于零，函数是减函数。

　　2. 最大值与最小值问题

　　Maxima and Minima Problems

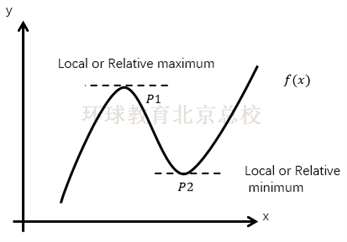
　　P1 is called a local or relative maximum point，p2 is called a local or relative maximum point.The gradient of the tangent line at a maxima or minima is zero, or does not exist.  

　　点P1称为局部最大值或相对最大值，P2称为局部最小值或相对最小值。最大或最小值处的切线斜率为零，或者斜率不存在。

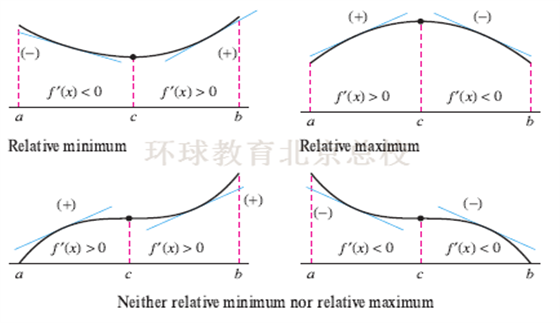
　　一阶导数测试是决定函数转折点性质的常规方法，假设函数f（x）在包含点C的区间内连续，点C的导数为零，或者C处不可导，

　　如果导数在穿过点c时由正变负，则函数在点C处有相对最大值；

　　如果导数在穿过点c时由负变正，则函数在点C处有相对最小值；

　　如果导数在点c两侧同时为正或为负，则函数在点C处没有相对极值出现。

　　常考题型解析

　　Example 2（求函数的相对极值/驻点问题）

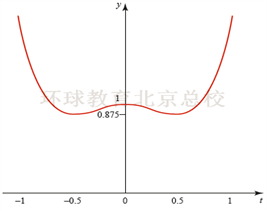
　　解题步骤：

　　1. 一阶导数为零，求出关键点；

　　2. 带回原函数，求出函数值；

　　3. 通过一阶段测试，觉得关键点的性质, 最大值，最小值，或者不是极值点。

　　函数的增减性与一阶导数紧密联系在一起，求函数的极值问题无论在考试中还是在生活应用中都是非常重要的。

　　
     小伙伴们觉得有用的话赶紧记起来，也别忘了关注我们呦，关注：http://beijing.gedu.org/我们会继续为大家分享A-level的相关信息，希望同学们都能A*通过～